আগের অধ্যায়ে আমরা বস্তুর গতি নিয়ে আলোচনা করেছি কিন্তু কেন বস্তু গতিশীল হয় সেটি নিয়ে কিছু বলা হয়নি। এই অধ্যায়ে আমরা দেখব বস্তু গতিশীল হয় বলের কারণে এবং বল নিয়ে আইজ্যাক নিউটনের তিনটি যুগান্তকারী সূত্র নিয়ে আলোচনা করব। বল কীভাবে বস্তুর উপর কাজ করে সেটি নিয়ে আলোচনা করার সময় খুব স্বাভাবিকভাবেই বিভিন্ন ধরনের বল, বস্তুর জড়তা, বলের প্রকৃতি, ঘর্ষণ বল এই বিষয়গুলোও আলোচনায় উঠে আসবে।
পৃথিবীতে কত ধরনের বল আছে জিজ্ঞেস করা হলে তোমরা নিশ্চয়ই বলবে অনেক ধরনেরা কোনো কিছুকে যদি ধাক্কা দিই সেটা একটা বল, ট্রাক যখন বোঝা টেনে নিয়ে যায় সেটা একটা বল, ঝড়ে যখন গাছ উপড়ে পড়ে সেটা একটা বল, চুম্বক যখন লোহাকে আকর্ষণ করে সেটা একটা বল, বোমা বিস্ফোরণে যখন ঘরবাড়ি উড়িয়ে দেয় সেটা একটা বল, ক্রেন যখন কোনো কিছুকে টেনে তুলে সেটা একটা বল। একটুখানি সময় দিলেই এ রকম নানা ধরনের বলের তোমরা একটা বিশাল তালিকা তৈরি করতে পারবে।
কিন্তু চমকপ্রদ ব্যাপারটি কী জানো? প্রকৃতিতে মাত্র চার রকমের বল রয়েছে, ওপরে যে তালিকা দেওয়া হয়েছে সেগুলোকে বিশ্লেষণ করা হলে দেখা যাবে এগুলো ঘুরে-ফিরে এই চার রকমের বাইরে কোনোটা নয়! আসলে মৌলিক বল মাত্র চারটি। সেগুলো হচ্ছে: মহাকর্ষ বল, তড়িৎ চৌম্বক বা বিদ্যুৎ চৌম্বকীয় বল, দুর্বল নিউক্লিয় বল ও সবল নিউক্লিয় বল।
এই সৃষ্টিজগতের সকল বস্তু তাদের ভরের কারণে একে অপরকে যে বল দিয়ে আকর্ষণ করে সেটাই হচ্ছে মহাকর্ষ বল। এই মহাকর্ষ বলের কারণে গ্যালাক্সির ভেতরে নক্ষত্ররা ঘুরপাক খায় কিংবা সূর্যকে ঘিরে পৃথিবী ঘোরে, পৃথিবীকে ঘিরে চাঁদ ঘোরে! পৃথিবীর মহাকর্ষ বল যখন আমাদের ওপর কাজ করে আমরা সেটাকে বলি মাধ্যাকর্ষণ। এই মাধ্যাকর্ষণ বল আমাদের পৃথিবীর কেন্দ্রের দিকে, অর্থাৎ নিচের দিকে টেনে রেখেছে এবং এর কারণেই আমরা নিজেদের ওজনের অনুভূতি পাই ।
পদার্থবিজ্ঞানের একটি চমকপ্রদ বল হচ্ছে মহাকর্ষ বল। ভর আছে সেরকম যেকোনো বস্তু অন্য বস্তুকে মহাকর্ষ বল দিয়ে আকর্ষণ করে। আমরা এই অধ্যায়ে মহাকর্ষ বল নিয়ে আরেকটু বিস্তারিতভাবে আলোচনা করব।
চিরুনি দিয়ে চুল আঁচড়ে সেটা দিয়ে কাগজের টুকরোকে আকর্ষণ করা বা চুম্বক দিয়ে অন্য চুম্বককে আকর্ষণ-বিকর্ষণ আমাদের অনেকেই কখনো না কখনো করেছি। যদিও তড়িৎ বা বিদ্যুৎ এবং চুম্বকের বলকে আলাদা ধরনের বল মনে হয় আসলে দুটি একই বল। শুধু দুইভাবে দেখা যায়। শুধু এই বলটা আকর্ষণ এবং বিকর্ষণ দুটোই করতে পারে, অন্যগুলো শুধু আকর্ষণ করতে পারে বিকর্ষণ করতে পারে না। মাধ্যাকর্ষণ শক্তির তুলনায় এটা অনেক শক্তিশালী (গুণ বা ট্রিলিয়ন ট্রিলিয়ন ট্রিলিয়ন গুণ শক্তিশালী!) কথাটা যে সত্যি সেটা নিশ্চয়ই তোমরা অনুমান করতে পারবে, কারণ যখন একটা চিরুনি দিয়ে চুল আঁচড়ে একটা কাগজকে আকর্ষণ করে তুলে নাও তখন কিন্তু সেই কাগজটাকে পুরো পৃথিবী তার সমস্ত ভর দিয়ে তৈরি মাধ্যাকর্ষণ বল দিয়ে টেনে রাখার চেষ্টা করে, তবু তোমার চিরুনির অল্প একটু বিদ্যুৎ সেই বিশাল পৃথিবীর পুরো মাধ্যাকর্ষণকে হারিয়ে দেয়।
এটাকে দুর্বল বলা হয় কারণ এটা তড়িৎ চৌম্বক বল থেকে দুর্বল (প্রায় ট্রিলিয়ন গুণ) কিন্তু মোটেও মহাকর্ষ বলের মতো এত দুর্বল নয়। মহাকর্ষ এবং তড়িৎ চৌম্বক বল যেকোনো দূরত্ব থেকে কাজ করতে পারে কিন্তু এই বলটা খুবই অল্প দূরত্বে ( m) কাজ করে! তেজস্ক্রিয় নিউক্লিয়াস থেকে যে বেটা (β) রশ্মি বা ইলেকট্রন বের হয় সেটার কারণ এই দুর্বল নিউক্লিয় বল।
এটি হচ্ছে সৃষ্টিজগতের সবচেয়ে শক্তিশালী বল, তড়িৎ চৌম্বক বল থেকেও একশ গুণ বেশি শক্তিশালী কিন্তু এটাও খুবই অল্প দূরত্বে (m) কাজ করে। পরমাণুর কেন্দ্রে যে নিউক্লিয়াস রয়েছে তার ভেতরকার প্রোটন এবং নিউট্রনের নিজেদের মাঝে এই প্রচণ্ড শক্তিশালী বল কাজ করে নিজেদের আটকে রাখে। প্রচণ্ড বলে আটকে থাকার কারণে এর মাঝে অনেক শক্তি জমা থাকে। তাই বড় নিউক্লিয়াসকে ভেঙে কিংবা ছোট নিউক্লিয়াসকে জোড়া দিয়ে এই বলের কারণে অনেক শক্তি তৈরি করা সম্ভব। নিউক্লিয়ার বোমা সে জন্য এত শক্তিশালী। সূর্য থেকে আলোর তাপও এই বল দিয়ে তৈরি হয়।
বিজ্ঞানীরা ধারণা করেন, এই চার ধরনের বলের মূল এক জায়গায় এবং তাঁরা সবগুলোকে এক সূত্র দিয়ে ব্যাখ্যা করার চেষ্টা করছেন। তড়িৎ চৌম্বক (বিদ্যুৎ চৌম্বকীয়) এবং দুর্বল নিউক্লিয়ার বলকে এর মাঝে একই সূত্র দিয়ে ব্যাখ্যা করা সম্ভব হয়েছে এবং সেটি তাত্ত্বিক পদার্থবিজ্ঞানের একটি আকাশছোঁয়া সাফল্য! (কাজেই তুমি ইচ্ছে করলে বলতে পারো বল তিন ধরনের: মহাকর্ষ, ইলেকট্রো উইক (Electro-weak) এবং নিউক্লিয়ার বল। কেউ এটাকে ভুল বলতে পারবে না!) অন্যগুলোকেও এক সূত্রে গাঁথার জন্য বিজ্ঞানীরা কাজ করে যাচ্ছেন ।
বল একটি ভেক্টর, কাজেই কোনো বস্তুর উপর যদি বল প্রয়োগ করা হয় তাহলে বিপরীত দিক থেকে অন্য একটি বল প্রয়োগ করে সেই বলটিকে কাটাকাটি করে দেওয়া সম্ভব। আমরা তখন বলি বলটি সাম্যাবস্থায় আছে। দুই বা ততোধিক বল একটি বস্তুর উপর প্রয়োগ করার পর বলগুলোর সম্মিলিত লব্ধি যদি শূন্য হয় তাহলে বস্তুটি স্থির থাকে।
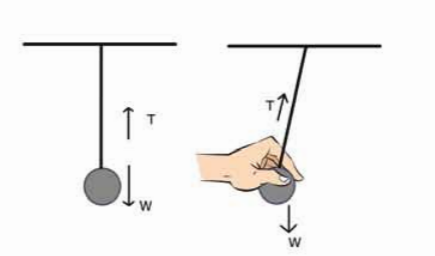
চিত্র 3.02:প্রথম ছবিতে বলের একটি সাম্যাবস্থা আছে।দ্বিতীয় ছবি পেন্ডুলাম ছেরে দেওয়া মাত্র একটি লব্ধি বল কাজ করবে, যে কারণে পেন্ডুলামটি নরতে শুরু করবে
চিত্র 3.02: চিত্রে দেখানো হচ্ছে একটা বস্তুকে সুতা দিয়ে ঝুলিয়ে দেওয়া আছে। বস্তুটির উপর পৃথিবীর আকর্ষণ বল (অর্থাৎ বস্তুর ওজন W), সোজা নিচের দিকে কাজ করছে। আবার আরেকটি বল যা সুতার টান খাড়া উপরের দিকে কাজ করছে। এখানে দুটি বল, একটি আরেকটির বিপরীত দিকে কাজ করে পরস্পরকে নিষ্ক্রিয় করে সাম্যাবস্থার সৃষ্টি করেছে।
যদি এখন সুতাটিকে কেটে দেওয়া যায় তাহলে সুতার টান T আর বস্তুটির উপর কাজ করবে না। শুধু পৃথিবীর অভিকর্ষ বল বা ওজন নিচের দিকে কাজ করবে, এখানে অভিকর্ষ বল বস্তুর ওজন হচ্ছে অসাম্য বল। এই অসাম্য বলের কারণে বস্তুটি মাধ্যাকর্ষণজনিত ত্বরণে নিচের দিকে পড়তে শুরু করবে।
সুতাটি না কেটেও আমরা বস্তুটির উপর অসাম্য বল প্রয়োগ করতে পারি। আমরা যদি বস্তুটিকে টেনে এক পাশে একটুখানি সরিয়ে নিই তাহলে ওজন আর সুতার টান বিপরীত দিকে থাকবে না, তখন সুতার টান আর বস্তুটির ওজন এই দুটি বল মিলে একটি লন্ধি বল কাজ করবে এবং বস্তুটি ছেড়ে দেওয়া মাত্র এই লন্ধি বলটি বস্তুটির উপর কাজ করতে শুরু করবে এবং বস্তুটি দুলতে থাকবে। এটি অসাম্য বলের আরেকটি উদাহরণ।
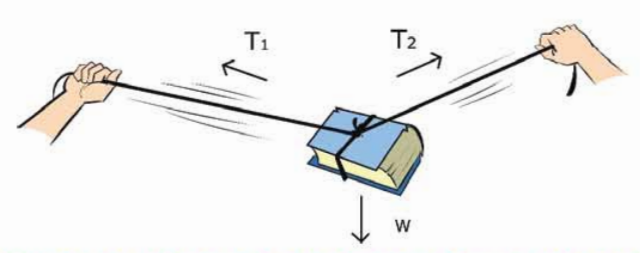
চিত্র 3.03: দুই পাশ থেকে তুমি যত জোরেই টানার চেষ্টা করো না কেন,তুমি কখনোই দড়িটা পুরোপুরি সোজা করতে পারবে না,কারণ তাহলে বইয়ের ওজনের বলটিকে নিষ্ক্রিয় করা যাবে না
তিনটি বল মিলেও সাম্যাবস্থা তৈরি করা যেতে পারে।যেমন, একটি ভারী বই একটি দড়ি দিয়ে বেঁধে দুই পাশ থেকে দড়ির দুই প্রান্ত টেনে ধরে বইটিকে স্থির অবস্থায় ঝুলিয়ে রাখা সম্ভব (চিত্র 3.03)। বইটি যেহেতু স্থির অবস্থায় আছে তাই এখানে বইটির ওজন W এবং দড়ির দুই প্রান্ডের দুটি টান এবং মিলে বলের লব্ধি শূন্য হবে।
ধরা যাক একটি ট্রাক এবং একটি বাইসাইকেল একই বেগে গিয়ে একটি ছোট গাড়িকে আঘাত করেছে। এই সংঘর্ষে সাইকেল নাকি ট্রাক, কোনটি ছোট গাড়িটার বেশি ক্ষতি করতে পারবে? অবশ্যই ট্রাক, কারণ তার ভর অনেক বেশি। সাইকেল এবং ট্রাক দুটোর বেগ এক হলেও ট্রাকের ভর অনেক বেশি, সেজন্য তার ভরবেগ অনেক বেশি। ভরবেগ সহজভাবে ভর এবং বেগের গুণফলকে বলা হয়। ভর যদি m হয় এবং বেগ যদি v হয় তাহলে ভরবেগ p হচ্ছে:
এখানে ভর স্কেলার রাশি, কিন্তু বেগ ভেক্টর, তাই ভরবেগ ভেক্টর। তোমরা ধারণা করতে পারো যে সাধারণভাবে যেহেতু কোনো কিছুর ভরের পরিবর্তন হয় না তাই ভরবেগের পরিবর্তন হতে পারে শুধু বেগের পরিবর্তন থেকে। কিন্তু আমরা বিশেষ কোনো ক্ষেত্রে দেখতে পারি গতিশীল কোনো কিছু বেগের পরিবর্তন হয়নি, কিন্তু ভরের পরিবর্তন হওয়ার কারণে তার ভরবেগের পরিবর্তন হয়ে গেছে। তোমাদের মনে হতে পারে ভরবেগ নামে নতুন একটা রাশির প্রচলন না করে এটিকে সব সময় ভর এবং বেগের গুণফল হিসেবে বিবেচনা করা হলে কী সমস্যা ছিল? সাধারণভাবে বড় কোনো সমস্যা না থাকলেও আলোর কণার ব্যাপারে এটি অনেক বড় সমস্যা হতে পারে। আলোর কণা বা ফোটনের কোনো ভর নেই কিন্তু তার ভরবেগ আছে। অর্থাৎ ভর এবং বেগ থেকে ভরবেগ বেশি মৌলিক একটি রাশি।
ভরবেগের একক হলো kg m/s
ভরবেগের মাত্রা হলো
যদি একাধিক বস্তু গতিশীল হয় এবং তারা ভিন্ন ভিন্ন বেগে যেতে থাকে তাহলে তাদের একটা সম্মিলিত ভরবেগ থাকে। বস্তুগুলোর ভিন্ন ভিন্ন বেগ থাকার কারণে চলার পথে একটির সাথে অন্যটির সংঘর্ষ হতে পারে এবং সংঘর্ষের কারণে তাদের বেগের পরিবর্তনও হতে পারে। কিন্তু যদি বাইরে থেকে কোনো বল প্রয়োগ করা না হয় তাহলে সংঘর্ষের পরেও সম্মিলিত ভরবেগের কোনো পরিবর্তন হয় না। এই প্রক্রিয়াটির নাম ভরবেগের নিত্যতার সূত্র।
সংঘর্ষ বা সংঘাত বলতে অতি অল্পসময়ের জন্য বৃহৎ কোন বল ক্রিয়া করে বস্তুর গতির হঠাৎ ও ব্যাপক পরিবর্তন করাকে বোঝায়। ক্রিকেট ব্যাট দিয়ে বলকে আঘাত করা, ক্যারামের স্ট্রাইকার দিয়ে গুটিকে আঘাত করা, কামান থেকে গোলা নিক্ষেপ, ইত্যাদি এর অন্তর্গত।
মনে করি, একটি সমতলে এবং ভর এবং বেগে সরলরেখায় যাচ্ছে। তাদের বেগের ভিন্নতার কারণে ধরা যাক তাদের মাঝে সংঘর্ষ হলো এবং সে কারণে তাদের বেগ পাল্টে গেল, ভরটির বেগ এখন এবং ভরটির বেগ । আমরা কি সংঘর্ষের পর বেগ এবং কত, সেটা বের করতে পারব?
সংঘর্ষের আগে ভর দুটির সম্মিলিত ভরবেগ
সংঘর্ষের পর ভর দুটির সম্মিলিত ভরবেগ
যেহেতু বাইরে থেকে কোনো বল দেওয়া হয়নি তাই সংঘর্ষের আগে যেটুকু ভরবেগ ছিল সংঘর্ষের পরেও সেটুকু ভরবেগ থাকবে। এটা হচ্ছে ভরবেগের সংরক্ষণশীলতা বা নিত্যতা।
কাজেই আমরা লিখতে পারি
এখানে একটি মাত্র সমীকরণ এবং দুটো অজানা রাশি এবং , কাজেই আমরা এবং বের করতে পারব না। যদি এবং বের করতে চাই তাহলে আরেকটা সমীকরণ দরকার, সৌভাগ্যক্রমে আমাদের আরো একটি সমীকরণ আছে। পরের অধ্যায়ে আমরা যখন শক্তি সম্পর্কে জানব তখন শক্তির নিত্যতার সূত্র থেকে দ্বিতীয় শক্তির সংরক্ষণশীলতার সূত্র থেকে আরেকটি সমীকরণ পেয়ে যাব, সেটি হচ্ছে শক্তির সংরক্ষণশীলতার সূত্র । তোমরা পরের অধ্যায়ে দেখবে m ভরের কোনো বস্তু যদি বেগে যায় তাহলে তার গতি শক্তি । কাজেই আমরা শন্তির সংরক্ষণশীলতা ব্যবহার করে লিখতে পারি:
সূত্র দুটোর দিকে তাকিয়েই তুমি বলতে পারবে দুটোর ভর যদি সমান হয়, অর্থাৎ তাহলে এবং অর্থাৎ বস্তু দুটো একটি অন্যটির সাথে তাদের বেগ পাল্টে নেয়।
দুটি বস্তুর সংঘর্ষের পর তাদের বেগ কত হয় সেটি ব্যবহার করে আমরা সরক দুঘটনার বিষয়গুলো খুব সহজে ব্যাখ্যা করতে পারবো
আমরা পরের অধ্যায়ে শক্তি সম্পর্কে জানার সময় পতিশক্তির বিষয়টি বিস্তারিতভাবে বুঝতে পারব কিন্তু “সংঘর্ষ” পড়ার সময় এর মাঝে জেনে গেছি যে গতিশক্তিকে হিসেবে প্রকাশ করতে হয়। ভ্রমণ সম্পর্কে আলোচনা করার জন্য বিষয়টি খুবই গুরুত্বপূর্ণ। শক্তির মাঝে বেগের বর্গ রয়েছে, যার অর্থ বেগ দ্বিগুণ করা হলে শক্তি চার গুণ বেড়ে যায়। যখন দুটো গাড়ির মাঝে সংঘর্ষ হয় তখন এই শক্তিটির কারণেই গাড়ি ক্ষতিগ্রস্ত হয় এবং আরোহীরা আঘাত পায়। কাজেই দুর্ঘটনার সময় ক্ষতি কমানোর সবচেয়ে সহজ উপায় হচ্ছে গতি কম রাখা। আমাদের দেশের বেশিরভাগ দুর্ঘটনা হয় গাড়ির বেগ বেশি রাখার কারণে। তখন গাড়িকে নিয়ন্ত্রণ করাও কঠিন হয় এবং দুর্ঘটনা ঘটার সময় সেখানে অনেক শক্তি ব্যয় হয়।
ধরা যাক পথে একটি অনেক ভারী পাথর বোঝাই ট্রাকের () সাথে একই বেগে আসা ছোট একটা গাড়ির () মুখোমুখি সংঘর্ষ হন। কে বেশি ক্ষতিগ্রস্ত হবে?
যেহেতু মুখোমুখি সংঘর্ষ হয়েছে তাই ছোট গাড়ির বেল ট্রাকের বেগের বিপরীত।
অর্থাৎ ট্রাকের বেগ হলে গাড়ির বেগ – u
যেহেতু ছোট গাড়ির ভর ট্রাকের ভর এর তুলনায় অনেক কম সেটাকে শূন্য ধরে নিলে খুব বেশি ভুল হবে না কিন্তু আমাদের হিসাবটি খুব সহজ হবে। (তুমি ইচ্ছা করলে সত্যিকারের বাস-ট্রাক এবং ছোট গাড়ির ভর নিয়ে হিসাবটি করে দেখতে পারো) 12 কে শূন্য ধরে আমরা দেখি সংঘর্ষের পর ট্রাকের বেগ
ফলাফলটি খুবই ভীতিজনক। সংঘর্ষের পর ট্রাকটি একই বেগে যেতে থাকবে, অর্থাৎ সংঘর্ষের ভয়াবহতা অনুভব করবে না। ছোট গাড়িটির বেগ –u থেকে পরিবর্তিত হয়ে 3u হয়ে যাবে যার অর্থ বেগের পরিবর্তন 3u - (-u) = 4u , ছোট গাড়ির বেগের দিক পরিবর্তিত হয়ে উল্টোদিকে চার গুণ বেগে ছিটকে যাবে। এই প্রক্রিয়ার ছোট গাড়িটি দুমড়েমুচড়ে ধ্বংস হয়ে যাবে এবং আরোহীদের প্রাণ হারানো হবে খুবই স্বাভাবিক ঘটনা।
কাজেই আমাদের পথে ভারী ট্রাক এবং ভারী বাস খুব সতর্ক হয়ে চালাতে হবে, কারণ দুর্ঘটনায় তারা বেশি ক্ষতিগ্রস্ত না হলেও তাদের সাথে মুখোমুখি সংঘর্ষ হলে ছোট গাড়ি অনেক বেশি ক্ষতিগ্রস্ত হয়।
ফুটবলের মাঠে আমরা সব সময়ই একজন খেলোয়াড়কে একটা স্থির ফুটবলকে কিক করে সেটা গতিশীল করে দূরে পাঠিয়ে দিতে দেখেছি। কিক করার সময় যখন ফুটবলটি স্পর্শ করে শুধু সেই মূহুর্তটিতে ফুটবলটিতে বল প্রয়োগ করা হয়, সেই বলের কারণে স্থির ফুটবলটি গতিশীল হয়।
আমরা শুধু এক মূহূর্তের জন্য বল প্রয়োগ না করে দীর্ঘ সময়ের জন্যও বল প্রয়োগ করতে পারি। একটা স্থির ঠেলাগাড়িকে বেশ কিছুক্ষণ ঠেলে তার ভেতরে একটা গতি তৈরি করে ছেড়ে দিতে পারি । ঘর্ষণের কারণে থেমে না যাওয়া পর্যন্ত সেটি বেশ খানিকক্ষণ গড়িয়ে যেতে পারে।
বল প্রয়োগ করে বেগের দিকও পরিবর্তন করা যায়। ক্রিকেট খেলার মাঠে যখন বোলার ব্যাটসম্যানের দিকে একটা ক্রিকেট বল ছুড়ে দেয়, ব্যাটসম্যান তখন ব্যাটের আঘাতে বলটিকে তার ব্যাট দিয়ে আঘাত করে বলটিকে সম্পূর্ণ অন্যদিকে পাঠিয়ে দিতে পারে।
উপরের তিনটি উদাহরণই আমরা দেখেছি অল্প সময় বা বেশি সময়ের জন্য কোনো কিছুর উপর বল প্রয়োগ করে তার বেগের পরিবর্তন করা হয়েছে। আমরা আগের অধ্যায়ে দেখেছি যে বেগে পরিবর্তনের হার হচ্ছে ত্বরণ। কাজেই বলা যেতে পারে কোনো বস্তুর উপর বল প্রয়োগ করা হলে তার ত্বরণ হয়। বস্তুর উপর প্রয়োগ করা বল এবং ত্বরণের সম্পর্কটি হচ্ছে নিউটনের দ্বিতীয় সূত্র:
নিউটনের দ্বিতীয় সূত্র: বস্তুর ভরবেগের পরিবর্তনের হার তার উপর প্রযুক্ত বলের সমানুপাতিক এবং যেদিকে বল প্রয়োগ করা হয় ভরবেগের পরিবর্তনও ঘটে সেদিকে।
ধরা যাক কোনো একটা বস্তুর আদি বেগ ছিল u এবং t সময় পর সেই বেগ পরিবর্তিত হয়ে (বেড়ে কিংবা কমে) হয়েছে v , কাজেই ভরবেগের পরিবর্তন হচ্ছে:
কাজেই ভরবেগের পরিবর্তনের হার:
যেহেতু এখানে ধরে নিয়েছি ভরের কোনো পরিবর্তন হয়নি তাই এভাবে লিখতে পারি। তাছাড়া আমরা জানি ত্বরণ হচ্ছে
সুতরাং প্রয়োগ করা বল যদি F হয় তাহলে আমরা নিউটনের দ্বিতীয় সূত্রকে লিখতে পারি:
কিন্তু আমরা সূত্রটাকে সমানুপাতিকভাবে লিখতে চাই না, সমীকরণ হিসেবে লিখতে চাই! তাহলে একটা সমানুপাতিক ধ্রুব k ব্যবহার করে আমাদের লিখতে হবে
নিউটনের দ্বিতীয় সূত্রটির বেলায় এবারে একটা চমকপ্রদ ব্যাপার ঘটানো সম্ভব। যেহেতু বল বিষয়টাই এর আগে কোথাও ব্যাখ্যা করা হয়নি, (নিউটনের প্রথম সূত্র দিয়ে শুধু সেটার একটা ধারণা দেওয়া হয়েছে) দ্বিতীয় সূত্র দিয়ে এই প্রথম সেটাকে প্রথমবার পরিমাপ করা হবে। তাই ধ্রুবকের একটি মান দিতে হবে। আমরা বলতে পারি নিউটনের দ্বিতীয় সূত্র প্রয়োগ করার সময় সমানুপাতিক ধ্রুবককে 1 ধরা হলে যেটা পাব সেটাই হচ্ছে বলের পরিমাপ! কী সহজে একটা সমানুপাতিক সম্পর্ককে সমীকরণ বানিয়ে ফেলা যায়।
সুতরাং আমরা নিউটনের দ্বিতীয় সূত্রটাকে একটা সমীকরণ হিসেবে লিখতে পারি। বল যদি F হয় এবং সমানুপাতিক ধ্রুবককে যদি 1 ধরে নিই তাহলে
এই ছোট এবং সহজ সমীকরণটি যে পদার্থবিজ্ঞানের জগতে কী বিপ্লব করে দিতে পারে সেটি বিশ্বাস করা কঠিন।
বলের একক হচ্ছে নিউটন N
বলের মাত্রা হচ্ছে [F] =
এখানে মনে রাখতে হবে, নিউটনের দ্বিতীয় সূত্রটি শুধু রৈখিক গতির জন্য সত্যি নয়, এটি যেকোনো গতির জন্য সত্যি। আমরা মাধ্যাকর্ষণ বল সম্পর্কে জেনেছি, নিউটনের দ্বিতীয় সূত্র ব্যবহার করে মহাকর্ষ বলের কারণে সূর্যকে ঘিরে ঘুরতে থাকা গ্রহদের গতিও ব্যাখ্যা করতে পারব। তবে আমরা এই বইয়ে নিউটনের দ্বিতীয় সূত্রটি শুধু রৈখিক গতির মাঝে সীমাবদ্ধ রাখব।
একটি বস্তুর উপর যদি বল প্রয়োগ করা হয় তাহলে নিউটনের দ্বিতীয় সূত্র ব্যবহার করে খুব সহজে তার ত্বরণ বের করা যায়। (বলকে ভর দিয়ে ভাগ করা হলে ত্বরণ বের হয়ে যাবে) ত্বরণ জানা থাকলে গতির সূত্রগুলো ব্যবহার করে তার বেগ কিংবা অতিক্রান্ত দূরত্ব বের করা সম্ভব। অন্যভাবে আমরা বলতে পারি যে যদি আমরা কোনো বস্তুকে গতিশীল দেখি এবং তার স্বরণটুকু বের করতে পারি তাহলে তার ভর জানা থাকলে তার উপর কতটুকু বল প্রয়োগ করা হয়েছে সেটিও বের করা সম্ভব।
এবার আমরা কয়েকটি উদাহরণ দেখি
আমরা বল কী সেটা বলেছি (যেটা ত্বরণের জন্ম দেয়) সেটা কেমন করে পরিমাপ করতে হয় সেটাও বলেছি (ভর আর ত্বরণের গুণফল) কিন্তু এখনো তোমাদের সত্যিকার কোনো বলের সাথে পরিচয় করিয়ে দিইনি। পদার্থবিজ্ঞানের একটি চমকপ্রদ বল হচ্ছে মহাকর্ষ বল, ভর আছে সে রকম যেকোনো
বস্তু অন্য বস্তুকে মহাকর্ষ বল দিয়ে আকর্ষণ করে। ধরা যাক, দুটি ভর এবং তাদের মাঝে দূরত্ব r। তাহলে তাদের মাঝে যে বল সৃষ্টি হবে সেটাকে যদি আমরা বলি তাহলে
এখানে G হচ্ছে মহাকর্ষীয় ধ্রুবক এবং তার মান হচ্ছে:
এখানে মনে রাখতে হবে m1 ভরটি m2 কে নিজের দিকে F বলে আকর্ষণ করে আবার m2 ভরটি m1 কে নিজের দিকে আকর্ষণ করে।
এই দুটো ভরের একটা যদি আমাদের পৃথিবী হয় এবং আমরা যদি ধরে নিই তার ভর M এবং পৃথিবীর উপরে m ভরের অন্য একটা জিনিস রাখা হয় তাহলে পৃথিবী m ভরকে তার কেন্দ্রের দিকে F বলে আকর্ষণ করবে।
এই বলটিই আসলে বস্তুটির ওজন। মনে রাখতে হবে এখানে R পৃথিবীর কেন্দ্র থেকে m. ভরটি পর্যন্ত দূরত্ব। পৃথিবীপৃষ্ঠ থেকে m ভরের দূরত্ব নয়। যেহেতু পৃথিবীর ব্যাসার্ধ অনেক (প্রায় 6000 km) কাজেই পৃথিবীর পৃষ্ঠে ছোটখাটো উচ্চতাকে ধর্তব্যের মাঝে আনার প্রয়োজন নেই। পৃথিবীর কেন্দ্র থেকে দূরত্ব মাপা হয় কারণ যদি গোলাকার কোনো বস্তু হয় তাহলে তার সমস্ত ভর কেন্দ্রবিন্দুতে জমা হয়ে আছে ধরে নিলে কোনো ভুল হয় না। (তার কারণ পৃথিবীর প্রত্যেকটা বিন্দুই m ভরকে নিজের দিকে আকর্ষণ করে এবং সবগুলো আকর্ষণ একত্র করা হলে মনে হয় যেন পৃথিবীর সমস্ত ভরটুকুই কেন্দ্রবিন্দুতে জমা হয়ে আছে।)
পৃথিবীর মাধ্যাকর্ষণ বলের জন্য m ভরটি একটি ত্বরণ অনুভব করবে। মাধ্যাকর্ষণের জন্য যে ত্বরণ হয় সেটাকে a না লিখে লেখা হয় g সেটা আমরা আগেই বলেছি। কাজেই F = ma এর পরিবর্তে লিখতে পারি:
কিংবা,
পৃথিবীর ভর M = , পৃথিবীর ব্যাসার্ধ R =
আমরা এর আগের অধ্যায়েই গতির সমীকরণে g এর এই মান ব্যবহার করেছি, এখন তোমরা জানতে পারলে কেন g এর এই মান ব্যবহার করা হয়েছিল।
মাধ্যাকর্ষণজনিত ত্বরণ জানা থাকলে আমরা খুব সহজেই যেকোনো ভর m এর জন্য মাধ্যাকর্ষণ বল বের করতে পারব। সেটি হবে
একটি বস্তুর উপর মাধ্যাকর্ষণজনিত বলটি আসলে বস্তুটির ওজনা কাজেই একটি স্তর ব্যবহার করে আমরা অন্য একটি বস্তুর উপর বল প্রয়োগ করতে পারি। ছবিতে M স্তর ঝুলিয়ে রাখার জন্য তার উপর মাধ্যাকর্ষণ বল Mg নিচের দিকে কাজ করছে। সেটি একটি কপিকল এবং সুতো দিয়ে টেবিলের উপর রাখা m ভরটির উপর প্রয়োগ করা হচ্ছে। নিউটনের দ্বিতীয় সূত্র অনুযায়ী m ভরটির একটি ত্বরণ হবে। অর্থাৎ
এই ত্বরণ ব্যবহার করে আমরা টেবিলের উপর রাখা বস্তুটির গতি বিশ্লেষণ করতে পারব।
কোনো বল প্রয়োগ না করলে কী হয় সেটি আমরা জানতে পেরেছি নিউটনের প্রথম সূত্র থেকে। বল প্রয়োগ করলে কী হয় সেটা আমরা জেনেছি নিউটনের দ্বিতীয় সূত্র থেকে। যখন একটি বস্তু অন্য বস্তুর ওপর বল প্রয়োগ করে তখন বস্তু দুটির মাঝে কী ধরনের প্রতিক্রিয়া হয়, সেটি আমরা জানতে পারব নিউটনের তৃতীয় সূত্র থেকে। সূত্রটি এ রকম:
নিউটনের তৃতীয় সূত্র: যখন একটি বস্তু অন্য একটি বস্তুর ওপর বল প্রয়োগ করে তখন সেই বস্তুটিও প্রথম বস্তুটির ওপর বিপরীত দিকে সমান বল প্রয়োগ করে।
পদার্থবিজ্ঞানের বইয়ে সাধারণত যেভাবে নিউটনের তৃতীয় সূত্র লেখা হয়, “প্রত্যেকটি ক্রিয়ার (action) একটা সমান এবং বিপরীত প্রতিক্রিয়া (Reaction) থাকে”, আমরা এখানে সেভাবে লিখিনি। আমাদের এতক্ষণে যেহেতু বল সম্পর্কে খানিকটা ধারণা হয়েছে হঠাৎ করে বলকে “ক্রিয়া” কিংবা “প্রতিক্রিয়া” বললে বিভ্রান্তি হতে পারে! তার চেয়ে বড় কথা যারা নতুন পদার্থবিজ্ঞান শেখে তাদের প্রথম প্রশ্নই হয় যে যদি সকল ক্রিয়া (কোনো একটি বল) একটি বিপরীত প্রতিক্রিয়া (আরেকটি বল) থাকে তাহলে ক্রিয়া-প্রতিক্রিয়া একে অপরকে কাটাকাটি করে শূন্য হয়ে যায় না কেন! এ জন্য তৃতীয় সূত্রটিতে খুব স্পষ্ট করে লিখে দেওয়া দরকার, তৃতীয় সূত্র বলছে যে যদি দুটি বস্তু A এবং B থাকে তাহলে A যখন B বলের ওপর বল প্রয়োগ করে তখন B বল প্রয়োগ করে A এর ওপর! বিপরীত দুটি বল ভিন্ন ভিন্ন বস্তুতে কাজ করে, কখনোই এক বস্তুতে নয়। যদি একই বস্তুতে দুটি বল প্রয়োগ করা হতো শুধু তাহলেই একে অন্যকে কাটাকাটি করতে পারত। এখানে কাটাকাটির কোনো সুযোগ নেই।
কয়েকটা উদাহরণ দিলে বিষয়টা পরিষ্কার হবে। ধরা যাক ওপর থেকে আমরা m ভরের একটা বস্তু (আপেল) উপর থেকে ছেড়ে দিয়েছি । আমরা জানি পৃথিবীর মাধ্যাকর্ষণ বলের জন্য m. ভর পৃথিবীর দিকে একটা বল F অনুভব করবে:
আমরা আগেই দেখেছি এই বলটাকে mg হিসেবে লেখা যায়।
নিউটনের তৃতীয় সূত্র শেখার পর আমরা জানি ভরটিও বিশাল পুরো পৃথিবীটাকে নিজের দিকে আকর্ষণ করছো সেই বলটিও শুধু বিপরীত দিকে। আমরা এই বলটিকে নিয়ে মাথা ঘামাই না, তার কারণ এই বলটার কারণে পৃথিবীর কতটুকু ত্বরণ a হচ্ছে সেটা ইচ্ছে করলে বের করতে পারি:
এখানে M হচ্ছে পৃথিবীর ভর এবং a হচ্ছে পৃথিবীর ত্বরণ
কাজেই
যদি পৃথিবীর ভর M = kg হয় তাহলে আমরা যদি 1 kg ভরের একটা বস্তুর উপর থেকে ছেড়ে দিই তার জন্য পৃথিবীর ত্বরণ হবে
এটি এত ক্ষুদ্র যে কেউ এটা নিয়ে মাথা ঘামায় না! তুমি যখন পরেরবার কোনো জায়গায় লাফ দেবে তখন মনে রেখো নিচে পড়ার সময় পুরো পৃথিবীকে তুমি আকর্ষণ করে নিজের দিকে টেনে নিয়েছিলো (যত কমই হোক তুমি সারা পৃথিবীকে নিজের দিকে টেনেছিলে, সেটা নিয়ে একটু পর্ব করতে পারো।)
নিউটনের তৃতীয় সূত্র বোঝার সবচেয়ে সহজ উপায় হচ্ছে আমরা কীভাবে হাঁটি সেটা বোঝা। আমরা সবাই হাঁটতে পারি এর পেছনে কী পদার্থবিজ্ঞান আছে সেটা না জেনেই সবাই হাঁটে। কিন্তু ভোমরা যেহেতু পদার্থবিজ্ঞান শিখতে শুরু করেছ তোমাদের খুব সহজ একটা প্রশ্ন করা যায়। তুমি যেহেতু স্থির অবস্থা থেকে হাঁটতে পারো, কাজেই আসলে তোমার একটি ত্বরণ হচ্ছে, যার অর্থ তোমার উপর বল প্রয়োগ করা হচ্ছে। কিন্তু আমরা সবাই জানি কেউ আমাদের উপর বল প্রয়োগ করে না। আমরা নিজেরাই হাঁটি। কেমন করে সেটা সম্ভব?
নিউটনের তৃতীয় সূত্র না জানা থাকলে আমরা কখনোই হাঁটার বিষয়টা ব্যাখ্যা করতে পারতাম না। আমরা যখন হাঁটি তখন আমরা পা দিয়ে মাটিতে ধাক্কা দিই (অর্থাৎ বল প্রয়োগ করি) তখন মাটিটা নিউটনের তৃতীয় সূত্র অনুযায়ী আমাদের শরীরে সমান এবং বিপরীত বল প্রয়োগ করে । এই সমান এবং বিপরীত বলটা দিয়েই আমাদের ত্বরণ হয়, আমরা হাঁটি!
বিষয়টা যাদের বুঝতে একটু সমস্যা হচ্ছে তাদেরকে মনে করিয়ে দেওয়া যায়, শক্ত মাটিতে হাঁটা সোজা কিছু ঝুরঝুরে বালুর উপর হাঁটা সোজা না। তার কারণ বালুর ওপর বল প্রয়োগ করা যায় না, বালু সরে যায়। তাই নিউটনের তৃতীয় সূত্রের পাল্টা বলটাও ঠিকভাবে পাওয়া যায় না। ব্যাপারটা আরো অনেক স্পন্ট করে দেওয়া যায় যদি কাউকে অসম্ভব মসৃণ একটা মেঝেতে সাবান পানি কিংবা তেল দিয়ে পিচ্ছিল করে হাঁটতে দেওয়া হয়। সেখানে ঘর্ষণ খুব কম, তাই আমরা পেছনে বল প্রয়োগ করতেই পারব না এবং সে জন্য তার প্রতিক্রিয়া হিসেবে আমাদের ওপর কোনো বলও পাব না। তাই হাঁটতেও পারব না (বিশ্বাস না হলে চেষ্টা করে দেখতে পারো)। বল প্রয়োগ করলে বিপরীত ব সমান বল পাওয়া যায়, যদি প্রয়োগ করতেই না পারি তাহলে তার প্রতিক্রিয়া বল পাব কেমন করে? আর হাঁটব কেমন করে?
আমরা এর আগে মহাকর্ষ কিংবা মাধ্যাকর্ষণ বল এবং স্প্রিংয়ের বল নিয়ে আলোচনা করেছি, এবারে সম্পূর্ণ ভিন্ন একটি বল নিয়ে আলোচনা করব, সেটি হলো ঘর্ষ
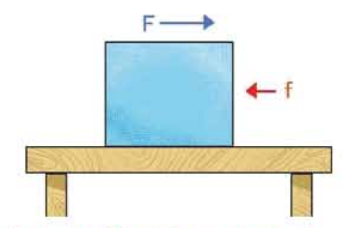
চিত্র 3.03:একটি ভরের উপর বল প্রয়োগ করলে ঘর্ষণের জন্যে বিপরীত দিকে
একটি বল তৈরি হতে পারে।
ধরা যাক, একটা টেবিলে কোনো একটা কাঠের টুকরো রয়েছে এবং সেই কাঠের টুকরোর ওপর বল প্রয়োগ করে সেখানে ত্বরণ সৃষ্টি করতে চাচ্ছি। ধরা যাক,3.03 চিত্রে যেভাবে দেখানো হয়েছে সেভাবে ভরটির ওপর বাম থেকে ডানে F বল প্রয়োগ করছি, দেখা যাবে কাঠের টুকরোয় টেবিলের সাথে কাঠের টুকরোর ঘর্ষণের কারণে একটা ঘর্ষণ বল f তৈরি হয়েছে এবং সেটি ডান থেকে বাম দিকে কাজ করে প্রয়োগ করা বলটিকে কমিয়ে দিচ্ছে।
এখন তুমি যদি মনে কর ঘর্ষণের ফলে ডান থেকে বাম দিকে একটা ঘর্ষন বল তৈরি হয় কাজেই কাঠের টুকরোর ওপরেও যদি বাম দিকে বল প্রয়োগ করি তাহলে প্রয়োগ করা বল আর ঘর্ষণ বল একই দিকে হওয়ার কারণে বাড়তি একটা বল পেয়ে যাব! কিন্তু দেখা যাবে এবারেও ঠিক বিপরীত দিকে ঘর্ষণ বল কাজ করছে। ঘর্ষণ বল সব সময়েই প্রয়োগ করা বলের বিপরীত দিকে কাজ করে৷ কাঠের টুকরোর ওপরে যদি খানিকটা ওজন বসিয়ে দিই দেখা যাবে ঘর্ষণ বল আরো বেড়ে গেছে, যদিও ওজন এবং ঘর্ষণ বল পরস্পরের ওপর লম্ব!
ঘর্ষণ বল কীভাবে তৈরি হয় ব্যাপারটা বুঝতে পারলেই আমরা দেখব এতে অবাক হবার কিছু নেই। যদিও আপাতদৃষ্টিতে কাঠ, টেবিলকে (কিংবা যে দুটো তলদেশের মাঝে ঘর্ষণ হচ্ছে) অনেক মসৃণ মনে হয় কিন্তু অণুবীক্ষণ যন্ত্র দিয়ে দেখলে দেখা যাবে সব তলদেশেই এবড়োখেবড়ো এবং এই এবড়োথেবড়ো অংশগুলো একে অন্যকে স্পর্শ করে বা খাঁজগুলো একে অন্যের সাথে আটকে যায়, সেটার কারণেই গতি বাধাপ্রাপ্ত হয় এবং আমরা বলি বিপরীত দিক থেকে ধর্ষণ বলের জন্ম হয়েছে। যদি দুটো তলদেশকে আরো চাপ দেওয়া হয় তাহলে এবড়োখেবড়ো অংশ আরো বেশি একে অন্যকে স্পর্শ করবে, একটির খাঁজ অন্যটির আরো গভীর খাঁজে ঢুকে যাবে এবং ঘর্ষণ বল আরো বেড়ে যাবে।
ঘর্ষণের জন্য তাপ সৃষ্টি হয়। সেটা অনেক সময়েই সমস্যা। যেমন গাড়ির সিলিন্ডারে পিস্টনকে ওঠানামা করার সময়ে সেখানে ঘর্ষণের জন্য তাপের সৃষ্টি হয় আর সেই তাপ নিয়ন্ত্রণ করার জন্য গাড়ির ইঞ্জিনকে শীতল রাখতে হয়। তাই সেখানে ঘর্ষণ কমানোর জন্য নানা ধরনের ব্যবস্থা নেওয়া হয়।
ঘর্ষণকে চারভাবে ভাগ করা যায়। স্থিতি ঘর্ষণ, গতি ঘর্ষণ, আবর্ত ঘর্ষণ এবং প্রবাহী ঘর্ষণ:
স্থিতি ঘর্ষণ (Static Friction): দুটো বস্তু একে অন্যের সাপেক্ষে স্থির থাকা অবস্থায় যে ঘর্ষণ বল থাকে সেটা হচ্ছে স্থিতি ঘর্ষণ। স্থিতি ঘর্ষণের জন্য আমরা হাঁটতে পারি, আমাদের পা কিংবা জুতোর তলা মাটিতে স্থিতি ঘর্ষণের কারণে আটকে থাকে এবং পিছলে পড়ে যাই না!
গতি ঘর্ষণ (Sliding Friction) : একটি বস্তুর সাপেক্ষে অন্য বস্তু যখন চলমান হয় তখন যে ঘর্ষণ বল তৈরি হয় সেটি হচ্ছে গতি ঘর্ষণ। সাইকেলের ব্রেক চেপে ধরলে সেটি সাইকেলের চাকাকে চেপে ধরে এবং ঘুরন্ত চাকাকে গতি ঘর্ষণের কারণে থামিয়ে দেয়। গতি ঘর্ষণ ওজনের উপর নির্ভর করে, ওজন যত বেশি হবে গতি ঘর্ষণ তত বেশি হবে। যদি কোনো কিছুর ভর M হয় তাহলে তার ওজন একটি বল, যার পরিমাণ w = Mg। তাহলে গতি ঘর্ষণ f কে লিখতে পারি f = W এখানে গতি ঘর্ষণ সহগ।
আবৰ্ত ঘর্ষণ (Rolling Friction) : একটি তলের উপর যখন অন্য একটি বস্তু পড়িয়ে বা ঘুরতে ঘুরতে চলে তখন সেটাকে বলে আবর্ত ঘৰ্ষণ। সবগুলো ঘর্ষণ বলের মধ্যে এটা সবচেয়ে ছোট ।আমরা সব সময়ই সকল রকম যানবাহনের মাঝে চাকা লাগিয়ে নিই। চাকা লাগানো স্যুটকেস খুব সহজে টেনে নেওয়া যায়, যদি এর চাকা না থাকত তাহলে মেঝের উপর টেনে নিতে আমাদের অনেক বেগ পেতে হতো।
প্রবাহী ঘর্ষণ (Fluid Friction) : যখন কোনো বস্তু তরল বা বায়বীয় পদার্থ (Fluid) এর ভেতর দিয়ে যায় তখন সেটি যে ঘর্ষণ বল অনুভব করে সেটি হচ্ছে প্রবাহী ঘর্ষণ। প্যারাস্যুট নিয়ে যখন কেউ প্লেন থেকে ঝাঁপিয়ে পড়ে তখন বাতাসের প্রবাহী ঘর্ষণের কারণে ধীরে ধীরে নিচে নেমে আসতে পারে ।
আমরা আগেই বলেছি ঘর্ষণ বল সব সময়ই প্রয়োগ করা বলের বিপরীত দিকে কাজ করে। সেজন্য স্বাভাবিকভাবেই ঘর্ষণ বল গতিকে কমিয়ে দেয় এবং আমাদের ধারণা হতে পারে আমরা সর্বক্ষেত্রে বুঝি ঘর্ষণ কমানোর চেষ্টা করি। কিন্তু সেটি সত্যি নয়। তোমরা নিশ্চয়ই কখনো না কখনো কাদার মাঝে কোনো গাড়ি বা ট্রাককে আটতে যেতে দেখেছ। তখন গাড়ির চাকা ঘুরলেও ঘর্ষণ কম বলে কাদা থেকে গাড়ি বা ট্রাক উঠে আসতে পারে না। ঢাকা পিছলিয়ে যায়। তখন গাড়ি বা ট্রাকটিকে তুলে আনার জন্য অন্যভাবে ঢাকা এবং কাদার মধ্যে ঘর্ষণ বাড়ানোর চেষ্টা করা হয়।
টায়ারের পৃষ্ঠ: গাড়ির টায়ার এবং রাস্তার মাঝে ঘর্ষণ থাকে বলে রাস্তার উপর দিয়ে পাড়ি যেতে পারে, যদি এই ঘর্ষণ না থাকত তাহলে গাড়ির চাকা পিছলে যেত এবং পাড়ি সামনে যেতে পারত না । এই ঘর্ষণ বাড়ানোর জন্য গাড়ির টায়ারে অনেক ধরনের খাঁজ কাটা হয়। যারা গাড়ি চালায় তার সব সময় লক্ষ রাখে তাদের গাড়ির চাকার খাঁজ কমে মসৃণ হয়ে যাচ্ছে কি না। যদি মসৃণ হয়ে যায় তাহলে ব্রেক করার পরও গাড়ি না থেমে পিছলে এগিয়ে যাবে!
রাস্তার মসৃণতা: গাড়ির টায়ারের সাথে রাস্তার ধর্ষণ বাড়ানোর জন্য রাস্তাগুলো বিশেষভাবে তৈরি করা হয়। রাস্তা যদি ঠিক না থাকে তাহলে সেখানে গাড়ির চাকা পিছলিয়ে (skid) যেতে পারে। শীতের দেশে তুষারপাতের পর রাস্তায় বরফ জমে গেলে রাস্তা অসম্ভব পিচ্ছিল হয়ে যেতে পারে এবং দুর্ঘটনার পরিমাণ দশ গুণ থেকে বেশি হয়ে যায়। আমাদের দেশে রাস্তায় পানি জমে কিংবা ছোট নুড়িপাথর বা কাঁকড়ের কারণে রাস্তার ঘর্ষণ কমে যেতে পারে। তোমরা সবাই পিচঢালা পথ দেখেছ, এই পিচঢালার কারণে টায়ারের সাথে রাস্তার ঘর্ষণ বেড়ে যায়। একই সাথে বৃষ্টির পানি চুইয়ে রাস্তার ভেতরে যেতে পারে না বলে রাস্তা বেশি দিন ব্যবহার করা যায়।
গতি নিয়ন্ত্রণ এবং ব্রেকিং বল: যানবাহন চালানোর সময় প্রয়োজন অনুসারে গাড়ির গতি বাড়াতে এবং কমাতে হয়। গাড়ির গতি যখন কম থাকে তখন সেটি নিয়ন্ত্রণ করা সহজ হয়, তাই তোমরা সব সময়ই দেখে থাকবে রাস্তায় বাঁক নেওয়ার সময় বা অন্য গাড়িকে পাশ কাটিয়ে যাবার সময় ব্রেক করে গাড়ির গতি কমানো হয়। গাড়ির ব্রেক প্যাডেলে চাপ দিলে সেই চাপটি চাকার সাথে লাগানো “সু” বা প্যাডে স্থানান্তরিত হয় এবং সেটি গাড়ির চাকার ভেতরকার চাকভিটিতে চাপ দেয়। এই চাপের কারণে প্যাড এবং চাকতিতে ঘর্ষণ হয় এবং এই ঘর্ষণ বল পাড়ির ঢাকাকে থামিয়ে দেয়।
আমরা এর মাঝে জেনে গেছি যে আমাদের প্রয়োজনে ঘর্ষণকে কখনো বাড়াতে হয় এবং কখনো কমাতে হয়।
ঘর্ষণ কমানোর জন্য আমরা যেসব কাজ করি সেগুলো হচ্ছেঃ
1. যে পৃষ্ঠটিতে ঘর্ষণ হয় সেই পৃষ্ঠটিকে যত সম্ভব মসৃণ করা। মসৃণ পৃষ্ঠে গতি ঘর্ষণ কম।
2. তেল মবিল বা প্লিজ জাতীয় পদার্থ হচ্ছে পিচ্ছিলকারী পদার্থ বা লুব্রিকেন্ট। দুটি তলের মাঝখানে এই লুব্রিকেন্ট থাকলে ঘর্ষণ অনেকখানি কমে যায়।
3.চাকা ব্যবহার করে ঘর্ষণ কমানো যায়। কাচা ব্যবহার করা হলে বড় গতি ঘর্ষনের পরিবর্তে অনেক ছোট আবর্ত ঘর্ষণ দিয়ে কাজ করা যায়। ঘুরন্ত চাকাতে বল বিয়ারিং ব্যবহার করে সরাসরি ঘর্ষণের বদলে ছোট স্টিলের বলগুলোর আবর্তন বর্ষণের সাহায্যে ঘর্ষণ অনেক কমানো সম্ভব।
4. গাড়ি, বিমান এ ধরনের দ্রুতগামী যানবাহনের ডিজাইন এমনভাবে করা হয় যেন বাতাস ঘর্ষণ তৈরি না করে স্ট্রিম লাইন করা পৃষ্ঠদেশের উপর দিয়ে যেতে পারে।
5. যে দুটি পৃষ্ঠদেশে ঘর্ষণ হয় তারা যদি খুব অল্প জায়গায় একে অন্যকে স্পর্শ করে তাহলে ঘর্ষণ কমানো যায়।
6. আমরা দেখেছি ঘর্ষণরত দুটো পৃষ্ঠে বল প্রয়োগ করা হলে ঘর্ষণ বেড়ে যায়, কাজেই লম্বভাবে আরোপিত বল কমানো হলে ঘর্ষণ কমানো যায়।
ঘর্ষণ কমানোর জন্য যে প্রক্রিয়াগুলো করা হয় সেগুলো করা না হলে কিংবা তার বিপরীত কাজগুলো করা হলেই ঘর্ষণ বেড়ে যায়। তাই ধর্ষণ বাড়ানোর জন্য আমরা যেসব কাজ করি সেগুলো হচ্ছে:
1. যে দুটো তলে ঘর্ষণ হচ্ছে সেগুলো অমসৃপ বা খসখসে করে তোলা।
2. যে দুটো তলে ঘর্ষণ হয় সেগুলো আরো জোরে চেপে ধরার ব্যবস্থা করা ।
3. ঘর্ষণরত তল দুটোর মাঝে গতিকে থামিয়ে স্থির করে ফেলা, কারণ স্থির ঘর্ষণ গতি ঘর্ষণ থেকে বেশি ।
4. ঘর্ষণরত তলের মাঝে খাঁজ কাটা, বা ঢেউ খেলানো করা। তাহলে এটি তলদেশকে জোরে আঁকড়ে ধরতে পারে। পানি বা তরল থাকলে সেটি খাঁজে ঢুকে গিয়ে পৃষ্ঠদেশের ঘর্ষণ বাড়াতে পারে।
5. বাতাস বা তরলের ঘনত্ব বাড়ানো ।
6. বাতাস বা ভরলে ঘর্ষণরত পৃষ্ঠদেশ বাড়িয়ে দেওয়া
7. চাকা বা বল বিয়ারিং সরিয়ে দেওয়া।
আমরা সবাই নিশ্চয়ই লক্ষ করেছি যে ঘর্ষণের কারণে তাপশক্তি তৈরি হয়। শীতের দিনে আমরা হাত খসে হাত উত্তপ্ত করি। গাড়ির ইঞ্জিন যে গরম হয়ে উঠে সেটিও ঘটে ঘর্ষণের কারণে। কাজেই ঘর্ষণের কারণে অপ্রয়োজনীয় তাপ সৃষ্টি করে শক্তির অপচয় হয়। গাড়ি, প্লেন, জাহাজ, সাবমেরিনকে ঘর্ষণ বলকে পরাস্ত করে এগিয়ে যেতে হয়, সেখানেও অতিরিক্ত জ্বালানি খরচ করতে হয়। এভাবে দেখা হলে মনে হতে পারে ঘর্ষণ বুঝি আমাদের জীবনের একটি উপদ্রব ছাড়া আর কিছু নয়।
আবার আমরা এর মাঝে দেখেছি ঘর্ষণ আছে বলেই আমরা হাঁটতে পারি, রাস্তায় গাড়ি চলতে পারে, কাগজে পেনসিল কলম দিয়ে লিখতে পারি, দালান গড়ে তুলতে পারি, প্যারাস্যুট দিয়ে নিরাপদে নিচে নামতে পারি। আমরা এ ধরনের অসংখ্য উদাহরণ দিতে পারি যেখানে ঘর্ষণ না থাকলে আমরা আমাদের প্রয়োজনীয় কাজগুলো করতে পারতাম না ।
কাজেই ঘর্ষণকে উপদ্রব মনে করা হলেও আমাদের মেনে নিতে হবে এটি আমাদের জীবনের জন্য খুবই প্রয়োজনীয় একটি উপদ্রব।
এর আগের অধ্যায়ে আমরা বেগ, দ্রুতি, ত্বরণ (এবং মন্দন), অতিক্রান্ত দূরত্ব এবং তাদের একটির সাথে অন্যটির সম্পর্ক শিখেছি, গতির সমীকরণগুলো বের করেছি এবং গতিসংক্রান্ত সমস্যা সমাধান করতে সেগুলো ব্যবহারও করেছি। এই অধ্যায়ে আমরা বল প্রয়োগ করে কীভাবে গতির সৃষ্টি করা যায় কিংবা গতিকে প্রভাবিত করা যায় সেটি শিখব। আমরা নিউটনের প্রথম সূত্রটি দিয়ে শুরু করতে পারি:
নিউটনের প্রথম সূত্র: বল প্রয়োগ না করলে স্থির বস্তু স্থির থাকবে এবং সমবেগে চলতে থাকা বস্তু সমবেগে চলতে থাকবে। (বুঝতেই পারছ বেগ যেহেতু ভেক্টর তাই সমবেগে চলতে হলে দিক পরিবর্তন করতে পারবে না, সোজা সরলরেখায় সমান দ্রুতিতে যেতে হবে।)
নিউটনের প্রথম সূত্রের প্রথম অংশ নিয়ে কারো সমস্যা হয় না কারণ আমরা সব সময়ই দেখেছি স্থির বস্তুকে ধাক্কা না দেওয়া পর্যন্ত সেটা নিজে থেকে নড়ে না, স্থির থেকে যায়। দ্বিতীয় অংশটি নিয়ে সমস্যা, কারণ আমরা কখনোই কোনো চলন্ত বস্তুকে অনন্তকাল চলতে দেখি না। ধাক্কা দিয়ে কোনো বস্তুকে গতিশীল করে ছেড়ে দিলেও দেখা যায় কোনো বল প্রয়োগ না করলেও শেষ পর্যন্ত বস্তুটা থেমে যায়। আমাদের দৈনন্দিন জীবনের অভিজ্ঞতা থেকে মনে হয় যেকোনো কিছুকে সমবেগে চালিয়ে নিতে হলে ক্রমাগত বুঝি সেটাতে বল প্রয়োগ করে যেতে হয়। নিউটনের প্রথম সূত্র থেকে আমরা জানতে পেরেছি সেটা সত্যি নয়। সমবেগে চলতে থাকা কোনো বস্তু যদি থেমে যায় তাহলে বুঝতে হবে সেখানে কোনো না কোনোভাবে বল প্রয়োগ করা হয়েছে। ঘর্ষণ, বাতাসের বাধা এ রকম অনেক কিছু আসলে উল্টো দিক থেকে বল প্রয়োগ করে চলমান একটা বস্তুকে থামিয়ে দেয়। যদি সত্যি সত্যি সব বল বন্ধ করে দেওয়া যেত তাহলে আমরা সত্যিই দেখতে পেতাম সমবেগে চলতে থাকা একটা বস্তু অনন্তকাল ধরে চলছে।
বল প্রয়োগ না করা পর্যন্ত স্থির বস্তু যে স্থির থাকতে চায় কিংবা গতিশীল বস্তু যে গতিশীল থাকতে চায়, বস্তুর এই বৈশিষ্ট্যটাই হচ্ছে জড়তা।হঠাৎ গাড়ি চলতে শুরু করলে আমরা যেভাবে পেছনের দিকে একটা ঝাঁকুনি খাই সেটা হচ্ছে জড়তার উদাহরণ। শরীরের নিচের অংশ গাড়ির সাথে লেগে আছে। গাড়ির সাথে সাথে সেটা চলতে শুরু করেছে কিন্তু শরীরের ওপরের অংশ এখনো স্থির এবং স্থির থাকতে চাইছে! তাই শরীরের ওপরের অংশ পেছনের দিকে ঝাঁকুনি খাচ্ছে। যেহেতু এটা স্থির থাকার জড়তা তাই এটাকে বলে স্থিতি জড়তা।
গতি জড়তার কারণে আমরা মানুষজনকে চলন্ত বাস ট্রেন থেকে নামতে গিয়ে আছাড় খেতে দেখি। চলন্ত বাস ট্রেনের মানুষটির পুরো শরীরটাই গতিশীল, সে যখন মাটিতে পা দিয়েছে তখন নিচের অংশ থেমে গিয়েছে, ওপরের অংশ পতি জড়তার কারণে তখনো ছুটছে। তাই সে হুমড়ি খেয়ে পড়ছো ।
নিউটনের প্রথম সূত্রে প্রথমবার “বল” শব্দটা ব্যবহার করা হয়েছে কিন্তু মজার ব্যাপার হচ্ছে বল বলতে আমরা কী বোঝাই, সেটা এখনো বলা হয়নি। এটা যদি পদার্থবিজ্ঞানের বই না হয়ে অন্য কোনো বই হতো তাহলে “বল প্রয়োগ”-এর জায়গায় “শক্তি প্রয়োগ” কথাটা ব্যবহার করলেও বাক্যটায় অর্থের কোনো উনিশ-বিশ হতো না। কিন্তু যেহেতু এটা পদার্থবিজ্ঞানের বই, তাই আমরা এখানে শক্তি কথাটা ব্যবহার করতে পারব না। পদার্থবিজ্ঞানের ভাষায় শক্তি সম্পূর্ণ ভিন্ন একটা রাশি! এখানে আমাদের বল কথাটাই ব্যবহার করতে হবে! কিন্তু বল মানে কী? আমরা তো এখন পর্যন্ত বলের কোনো সংজ্ঞা দিইনি!
আসলে নিউটনের প্রথম সূত্রটাই বলের সংজ্ঞা হতে পারে! যার প্রয়োগের কারণে স্থির বস্তু চলতে শুরু করে আর সমবেগে চলতে থাকা বস্তুর বেগের পরিবর্তন হয় সেটাই হচ্ছে বল। নিউটনের প্রথম সূত্র থেকে বলটা কী, সেটা বুঝতে পারি কিন্তু পরিমাপ করতে পারি না। দ্বিতীয় সূত্র থেকে আমরা বল পরিমাপ করা শিখব।
তোমরা যখন তোমাদের দৈনন্দিন জীবনে নানা কাজে বল ব্যবহার করো তখন তোমাদের মনে হতে পারে কোনো কোনো বল প্রয়োগ করতে হলে স্পর্শ করতে হয় (ক্রেন দিয়ে ভারী জিনিস তোলা, কোনো কিছুকে ধাক্কা দেওয়া, কিংবা চলতে চলতে ঘর্ষণের জন্য চলন্ত বস্তুর থেমে যাওয়া) আবার তোমরা লক্ষ করেছ কোনো কোনো বল প্রয়োগের জন্য স্পর্শ করতে হয় না। কোনো কিছু ছেড়ে দিলে মাধ্যাকর্ষণ বলের জন্য নিচে পড়া, চুম্বকের আকর্ষণ!) কাজেই আমরা বলকে স্পর্শ এবং অস্পর্শ দুই ধরনের বলে ভাগ করতে পারি। কিন্তু তোমরা নিশ্চয়ই বুঝতে পারছ আমরা যেখানে স্পর্শ করছি বলে ধারণা করছি, সেখানে কিন্তু পরস্পরের অণু-পরমাণু, তাদের ঘিরে ঘূর্ণায়মান ইলেকট্রন সরাসরি স্পর্শ দিয়ে নয় তাদের তড়িৎ চৌম্বক বল দিয়ে একে অন্যের সাথে কাজ করছে। অন্য কথায় বলা যায় আমরা যদি পারমাণবিক পর্যায়ে চলে যাই তাহলে সব বলই অস্পর্শক, এক পরমাণু অন্য পরমাণুকে আকর্ষণ-বিকর্ষণ করে দূর থেকে, তাদেরকে আক্ষরিক অর্থে স্পর্শ করতে হয় না ।
আরও দেখুন...